Page en travaux !
Fluide
Fluide parfait
Fluide visqueux
Hydrostatique
L’hydrostatique concerne l’étude des fluides en équilibres (sans mouvement).
Principe fondamental de l’hydrostatique
Ce principe s’applique aux fluides incompressibles, dans le champ de pesanteur seul. Dans un fluide homogène, on a alors la relation suivante :
\(p+ \rho\times g \times z = constante\) (1)
où p, \(\rho\), g et z sont respectivement la pression, la masse volumique du fluide, l’accélération de la pesanteur et l’altitude en un point du fluide.
Cette relation peut également s’écrire, si l’on considère deux points du fluide notés A et B :
\(p_A+ \rho\times g \times z_A = p_B + \rho\times g \times z_B\) (2)
ou
\(p_B \,- \, p_A = \rho \times g \times (z_A – z_B)\) (3)
Exemple d’application (sujet U22, 2022, Station d’épuration)
- Partie B – Étude du circuit de recirculation des boues activées.
Le bon fonctionnement de cette station d’épuration par boues activées exige de bien séparer l’eau traitée de la masse de boue activée de manière à produire une eau clarifiée conforme aux normes de rejet. Cette séparation solide-liquide est réalisée par sédimentation gravitaire.
L’objectif de cette partie est d’étudier le circuit de recirculation des boues.
Le clarificateur 1 est à l’arrêt (isolé hydrauliquement du reste de l’installation et consigné électriquement). Partant du principe que la hauteur de l’ouvrage est décomposée en deux zones superposées assurant des fonctions différentes (figure ci-dessous).
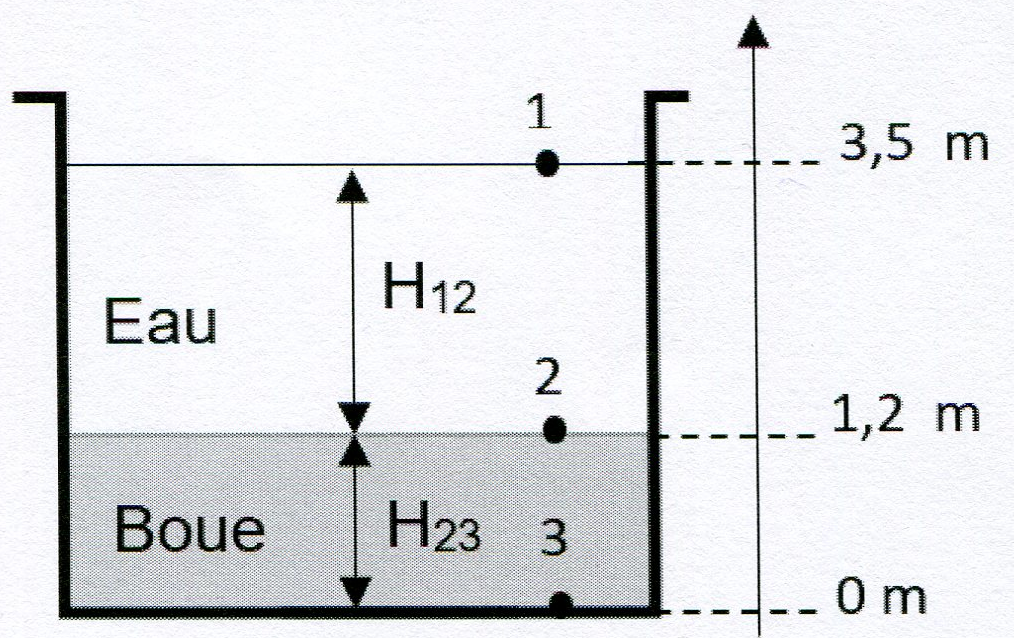
Données :
- la surface du clarificateur est à l’air libre
- surface dans le fond du clarificateur \(S_r=1870,4 \, m^2\)
- pression atmosphérique \(P_{atm} = 1013 \, hPa\)
- masse volumique de l’eau \(\rho_{eau}=1000\, kg \cdot m^{-3} \)
- masse volumique de la boue \(\rho_{boue} = 1003 \, kg \cdot m^{-3}\)
- accélération de la pesanteur \(g = 9,81 \, m \cdot s^{-2}\)
QB1 : donner l’expression littérale de la pression \(P_3\) dans le fond du clarificateur en fonction de \(g, P_{atm}, \rho_{boue},\rho_{eau} , H_{12} \, et \, H_{23}\), puis calculer la valeur de \(P_3\).
La pression tolérée par le sol est de \(3,0 \,daN \cdot cm^{-2}\).
QB2 : vérifier la conformité du bassin vis-à-vis de la pression au sol.
Corrigé
QB1
Remarquons tout d’abord que :
- le clarificateur contient des fluides dont les masses volumiques sont différentes ;
- les auteurs du sujet ont placé 3 points, 1, 2 et 3 ;
- on connait la pression en 1 : c’est la pression atmosphérique puisque « la surface du clarificateur est à l’air libre ».
On ne peut utiliser le Principe fondamental de l’hydrostatique que si le fluide est homogène. Nous allons donc l’utiliser une 1ère fois dans la zone délimitée par les points 1 et 2 ( eau) , puis une 2ème fois dans la zone délimitée par les points 2 et 2 et 3 ( boue).
La résolution est plus simple si l’on utilise le Principe fondamental de l’hydrostatique sous la forme : \(p_B \,- \, p_A = \rho \times g \times (z_A – z_B)\) mais on obtient bien sûr le même résultat quelle que soit la forme utilisée (Voir plus loin).
Entre 1 et 2 (eau)
\(p_2-p_1 = \rho_{eau} \times g \times (z_1 – z_2)\)
donc : \(p_2 \,= \, p_1 + \rho_{eau} \times g \times (z_1 – z_2)\) (4)
Entre 2 et 3 (boue :
\(p_3 \,- \, p_2 = \rho_{boue} \times g \times (z_2 – z_3)\)
donc : \(p_3 \,= \, p_2 + \rho_{boue} \times g \times (z_2 – z_3)\) (5)
En replaçant dans la relation (5) \(p_2\) par son expression (4), nous obtenons :
\(p_3 \,= \, p_1 + \rho_{eau} \times g \times (z_1 – z_2) + \rho_{boue} \times g \times (z_2 – z_3)\)
\(P_1 = P_{atm}\) et d’autre part \( z_1- z_2 =H_{12} \, et \ z_3-z_2 =H_{23}) \),
Donc : \(p_3 \,= \, p_{atm} + \rho_{eau} \times g \times H_{12} + \rho_{boue} \times g \times H_{23} \)
Même démarche en partant de la relation : \(p_A+ \rho\times g \times z_A = p_B + \rho\times g \times z_B\)
Entre 1 et 2 (eau) : \(p_1+ \rho_{eau}\times g \times z_1 = p_2 + \rho_{eau}\times g \times z_2\)
\(P_1 = P_{atm}\). La relation précédente peut donc s’écrire :
\(p_{atm}+ \rho_{eau}\times g \times z_1 = p_2 + \rho_{eau}\times g \times z_2\)
Soit : \(p_{atm}+ \rho_{eau}\times g \times z_1- \rho_{eau}\times g \times z_2 = p_2 \)
puis : \(p_{atm}+ \rho_{eau}\times g \times (z_1- z_2) = p_2 \)
puis : \( p_2 =p_{atm}+ \rho_{eau}\times g \times (z_1- z_2) \)
Enfin, en remarquant que \( z_1- z_2 =H_{12}\), nous obtenons : \( p_2 =p_{atm}+ \rho_{eau}\times g \times H_{12}\) (1)
Entre 2 et 3 (boue : \(p_2+ \rho_{boue}\times g \times z_2 = p_3 + \rho_{boue}\times g \times z_3\)
Soit : \(p_2+ \rho_{boue}\times g \times z_2-\rho_{boue}\times g \times z_3 = p_3 \)
puis : \(p_3=p_2+ \rho_{boue}\times g \times z_2-\rho_{boue}\times g \times z_3 \)
puis : \(p_3=p_2+ \rho_{boue}\times g \times (z_2- z_3 \)
En remarquant que \( z_2- z_3 =H_{23}\), nous obtenons :
\(p_3=p_2+ \rho_{boue}\times g \times H_{23} \) (2)
Il n’y a plus qu’à remplacer \(p_2\) en utilisant la relation (1) :
\(p_3=p_{atm}+ \rho_{eau}\times g \times H_{12}+ \rho_{boue}\times g \times H_{23} \)
Application numérique
\(p_{atm}\) doit tout d’abord être convertie en Pascal : \(p_{atm} =1013 \times 100 =101300 \, Pa\).
A partir du schéma du clarificateur nous obtenons : \(H_{12} = 2,3 m, \, H{23} = 1,2\,m \)
\(p_3=101300+ 1000 \times 9,81 \times 2,3+ 1003\times 9,81 \times 1,2\)
\(p_3= 1,36 \cdot 10^5 \,Pa\)
QB2
La pression tolérée par le sol est de \(3,0 \,daN \cdot cm^{-2}\).
Il nous faut convertir cette pression en Pa c’est-à-dire en \(N \cdot m^{-2}\)
1 daN = 10 N, la pression tolérée est donc égale à \(30 \, N \cdot cm^{-2}\)
\(1 \,cm = 10^{-2} \,m \, donc \, 30 \, N \cdot cm^{-2} = 30 \, N \cdot (10^{-2} \,m)^{-2}=30 \cdot 10^4 \, N \cdot m^{-2}\)
La pression tolérée par le sol est donc égale à \(30 \cdot 10^4 Pa\).
Nous avons déterminé précédemment la pression exercée sur le sol : \(p_3= 1,36 \cdot 10^5 \,Pa = 13,6\cdot 10^4 \,Pa\)
La pression exercée sur le sol est donc inférieure à la pression tolérée.
l
Dynamique des fluides
Théorème de Bernoulli
Nous considérons l’écoulement d’un fluide parfait dans une conduite. Le fluide étant parfait, sa masse volumique \(\rho\) est constante et il n’y a pas de frottement.
Dans cette conduite, nous examinons le mouvement d’un petit volume de fluide (de l’eau par exemple) se déplaçant du point 1 au point 2. Son altitude est notée z, sa masse m et sa vitesse v.
Conservation de l’énergie. – Le fluide étant parfait, l’énergie du petit volume d’eau reste constante lors de son déplacement de du point 1 au point 2.
Formes d’énergie. – L’énergie du petit volume de fluide, W, est composée de :
- de l’énergie cinétique : \(\frac{1}{2} \times m\times v^2 \)
- de l’énergie potentielle de pesanteur : \(\ m\times g \times z \)
- de l’énergie potentielle de pression : \(p\times V \)
\(W=m\times g \times z+p\times V+\frac{1}{2} \times m\times v^2 = constante \)
Écoulement permanent. – L’écoulement est dit « permanent » lorsque ses caractéristiques sont constantes au cours du temps.
Ligne de courant. – C’est la trajectoire suivie par un le centre d’unpetit volume de fluide. Sur l’animation ci-dessus, c’est la ligne rouge reliant les points 1 et 2.
Dans ces conditions, plutôt que de suivre le petit volume de fluide, on peut considérer un petit volume de fluide en A et un autre en B (même volume) et écrire qu’il ont la même énergie. On peut également écrire qu’en régime permanent l’énergie est constante le long d’une ligne de courant.
\(m\times g \times z_1+p_1\times V+\frac{1}{2} \times m\times v_1^2 =m\times g \times z_2+p_2\times V+\frac{1}{2} \times m\times v_2^2 \)
Cette relation est rarement (jamais ?) utilisée sous cette forme. Les physiciens lui préfèrent la forme suivante :
| Théorème de Bernoulli pour un écoulement permanent d’un point 1 à un point 2 : \(z_1+\frac{p_1}{\rho \times g}+\frac{v_1^2}{2\times g} = z_2+\frac{p_2}{\rho \times g}+\frac{v_2^2}{2\times g} \) |
Equation de continuité

Le schéma ci-dessus représente un conduit avec un rétrécissement en son centre (on parle d’un venturi). A l’intérieur de ce conduit, un fluide se déplace de la section 1 à la section 2. La totalité du fluide passant par la section 1 passera par la section 2. Si le fluide est un fluide parfait et si l’écoulement est permanent, le débit volumique de fluide dans la section 1, Q1 est égal au débit volumique dans la section 2, Q2. L’équation de continuité s’écrit :
\(Q_1 = Q_2\)
Par ailleurs, Le débit est lié à la vitesse du fluide et à la section de la manière suivante :
\(Q_1 = V_1 \times S_1\) et \(Q_2 = V_2\times S_2\)
L’équation de continuité peut donc s’écrire sous la forme :
\(V_1 \times S_1= V_2\times S_2\) ou \(V_2=V_1 \times \frac{S_1}{S_2}\)
S1 >S2 donc V2>V1
Écoulement Laminaire, écoulement turbulent
patience
ombre de Reynolds
Perte de charges
Patience
Théorème de Bernoulli généralisé
On considère maintenant qu’au cours de son écoulement le fluide peut perdre de l’énergie (moteur hydraulique, perte de charge… ou recevoir de l’énergie (pompe). Les perte de charge sont en général notées J, l’apport d’énergie Hmt.
Théorème de Bernoulli généralisé pour un écoulement permanent d’un point 1 à un point 2 :
\(z_1+\frac{p_1}{\rho \times g}+\frac{v_1^2}{2\times g}-J_{12}+H_{mt} = z_2+\frac{p_2}{\rho \times g}+\frac{v_2^2}{2\times g} \)
Utilisation de l’équation de Bernoulli
L’équation de Bernoulli est une relation. Il ne doit donc y avoir qu’une seule inconnue, en générale la vitesse en un point ou la pression en un point pour ce qui concerne l’équation de Bernoulli ou la hauteur manométrique d’une pompe pour ce qui concerne l’équation de Bernoulli généralisée
Il faut donc choisir judicieusement les points ou les sections 1 et 2
Remarquons que l’équation de continuité nous permet de calculer une vitesse dans une section si l’on connait la vitesse du fluide sur une autre section.
Exemple d’application : Venturi
Le schéma ci-dessous représente un conduit avec un rétrécissement en son centre (on parle d’un venturi).

Nous souhaitons déterminer la pression au point P2. Nous pouvons appliquer le théorème de Bernoulli pour l’écoulement entre les points P1 et P2 :
\(z_1+\frac{p_1}{\rho \times g}+\frac{v_1^2}{2\times g} = z_2+\frac{p_2}{\rho \times g}+\frac{v_2^2}{2\times g} \) (1)
Notons que les points 1 et 2 sont à la même altitude : \(z_1 = z_2 \)
Nous pouvons donc simplifier le théorème de Bernoulli :
\(\frac{p_1}{\rho \times g}+\frac{v_1^2}{2\times g} = \frac{p_2}{\rho \times g}+\frac{v_2^2}{2\times g} \) (2)
Puis isoler le terme contenant p2 :
\(\frac{p_2}{\rho \times g}=\frac{p_1}{\rho \times g}+\frac{v_1^2}{2\times g} -\frac{v_2^2}{2\times g} \) (3)
Par ailleurs, les vitesses aux points P1 et P2 sont liées par l’équation de continuité :
\( V_1 \times S_1=V_2 \times S_2\) (4)
donc \(V_2=\frac{ V_1 \times S_1}{S_2}\) (5)
En utilisant les relations (3) et (5) nous obtenons :
\(\frac{p_2}{\rho \times g}=\frac{p_1}{\rho \times g}-\frac{v_1^2}{2\times g} \times \frac{S_1^2-S_2^2}{2\times g\times S_2^2} \) (6)
Cette relation montre que la pression est plus basse dans la partie étroite du conduit que dans la partie large. Cela ne correspond pas à l’intuition. Cela est pourtant logique.
Dans la partie étroite du conduit, le fluide a une vitesse plus élevée, son énergie cinétique est donc plus élevée. L’énergie potentielle de pesanteur est constante le long de l’écoulement puisque le conduit est horizontal.
La somme Énergie cinétique + Énergie potentielle de pression + Énergie potentielle de pesanteur étant constante le long de l’écoulement, l’énergie potentielle de pression doit être plus faible dans la partie étroite du conduit.
Remarque : on peut montrer ce phénomène avec 2 feuilles de papier et un peu de souffle (demander à votre professeur ou cherchez sur internet).
Exemple d’application : Écoulementent aval d’une retenue d’eau
Le schéma ci-dessous représente une retenue d’eau (par exemple un barrage) et la conduite par laquelle s’écoule l’eau.
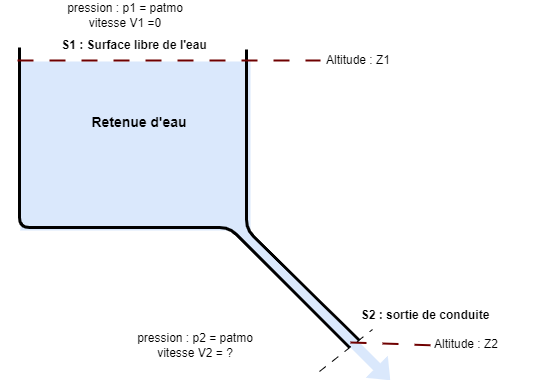
La surface libre de l’eau S1 est beaucoup plus importante que celle de la section de sortie S2. De ce fait, la vitesse d’écoulement de l’eau V1 est beaucoup plus petite que V2. On peut donc faire l’hypothèse que V1 = 0
En effet, l’équation de continuité nous permet d’écrire : \( V_1 \times S_1=V_2 \times S_2\)
donc \(V_1 =V_2 \times \frac{ S_2}{S_1}\)
S1 >> S2 donc \(\frac{ S_2}{S_1}\simeq0\) et \( V_1\simeq0\)
Ecrivons l’équation de Bernoulli pour l’écoulement de l’eau entre les sections S1 et S2 :
\(z_1+\frac{p_1}{\rho \times g}+\frac{v_1^2}{2\times g} = z_2+\frac{p_2}{\rho \times g}+\frac{v_2^2}{2\times g} \)
p1 = patmo, p2 = patmo, v1 = 0 donc
\(z_1+\frac{p_atmo}{\rho \times g}+\frac{0^2}{2\times g} = z_2+\frac{p_atmo}{\rho \times g}+\frac{v_2^2}{2\times g} \)
Soit :
\(z_1 = z_2+\frac{v_2^2}{2\times g}\)
Réorganisons la relation précédente :
\(v_2^2=2\times g\times (z_1 – z_2)\) soit : \(v=\sqrt{=2\times g\times(z_1 – z_2)}\)
C’est la formule deTorricelli.
Exemples d’application : circuit avec pompe
Sujet de Physique 2018 – STEP – unité pharmaceutique
Données :
Conduite de refoulement : diamètre d = 20,0 cm
Débit volumique de la pompe : Qv = \(400\, m^3 \cdot h^{-1}\)
Altitude des points 1 et 2 : \(Z_1\) et \(Z_2\)
Pression aux points 1 et 2 : \(P_1\) et \(P_2\)
Vitesse du fluide aux points 1 et 2 : \(v_1\) et \(v_2\)
Équation de Bernoulli pour un fluide en écoulement permanent d’un point 1 vers un point 2, dans une portion où se trouve une pompe de hauteur manométrique totale Hmt, les pertes de charge etant notées j :
\(z_1+\frac{p_1}{\rho \times g}+\frac{v_1^2}{2\times g}-J+H_{mt} = z_2+\frac{p_2}{\rho \times g}+\frac{v_2^2}{2\times g} \)
Les pertes de charge sont équivalentes à une hauteur de 1 m de liquide.
Puissance hydraulique d’une pompe de hauteur manométrique totale Hmt, assurant un débit de fluide \(Q_v\) :
\(P=Q_v \cdot \rho \cdot g \cdot H_{mt}\)
D.4 Déterminer la valeur du débit volumique Qv de l’eau en \(m^3 \cdot s^{-1}\)
D.5 Montrer que la vitesse d’écoulement de l’eau vaut environ \(3,54\, m \cdot s^{-1}\) à la sortie de la pompe.
La section du puits est très supérieure à la section de la conduite de refoulement.
D.6 Justifier que la vitesse d’écoulement au niveau de la surface du puits est négligeable devant la vitesse d’écoulement dans la conduite.
D.7 Montrer que la hauteur manométrique totale de la pompe est proche de 8,64 m en appliquant le théorème de Bernoulli entre le puits de stockage (point A) et la station de dépollution (point B). Le point B se situe a l’air libre.
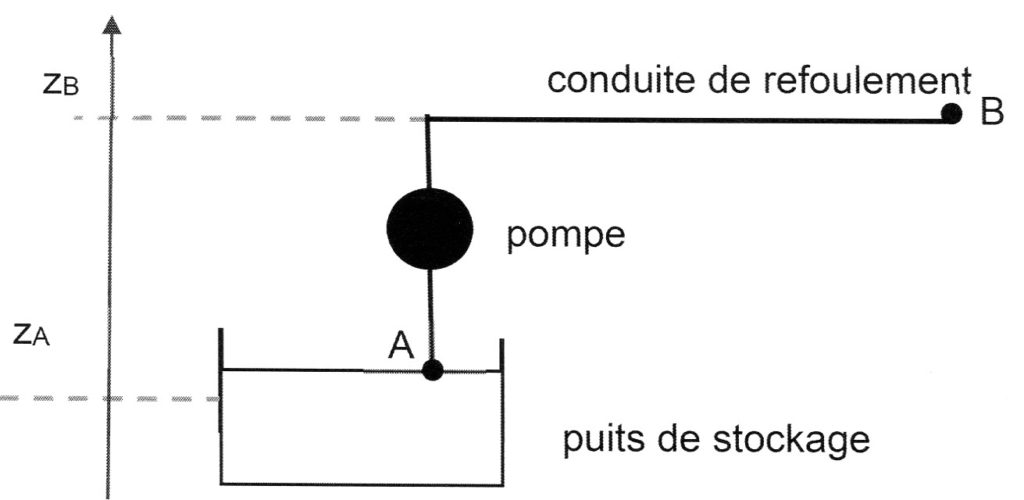
D.8 Calculer la puissance hydraulique que doit fournir la pompe.
Corrigé
D.4 Déterminer la valeur du débit volumique Qv de l’eau en \(m^3 \cdot s^{-1}\)
Qv = \(400\, m^3 \cdot h^{-1}\) => Qv de l’eau en \(m^3 \cdot s^{-1}\)
1 h = 3600 s donc : Qv = \(\frac{400}{3600}=0,111\,m^3 \cdot s^{-1}\)
D.5 Montrer que la vitesse d’écoulement de l’eau vaut environ \(3,54\, m \cdot s^{-1}\) à la sortie de la pompe.
\(Q=v\times S \Longleftrightarrow v =Q\frac{Q}{S} \)
On connait la valeur du débit Q, mais pas la valeur de S. Dans l’énoncé, il est indiqué : Conduite de refoulement : diamètre d = 20,0 cm
Donc d = 0,2m
La surface de la section droite de la conduite est calculée avec : \(S= \pi\times r^2\) ou avec \(S=\frac{ \pi\times d^2}{4}\)
Application numérique : \(S=\frac{ \pi\times 0,2^2}{4}=0,0314 \, m^2\)
\(v =Q\frac{Q}{S} \quad \quad Application \quad numérique : \, v =Q\frac{0,111}{0,0314} =3,54 /, m\cdot s^{-1} \)
Nous obtenons la valeur indiquée dans la question.
D.6 Justifier que la vitesse d’écoulement au niveau de la surface du puits est négligeable devant la vitesse d’écoulement dans la conduite.
L’équation de continuité \(Q_A = Q_B\) nous permet d’écrire : \( V_A \times S_A=V_B \times S_B\)
donc \(V_A =V_B \times \frac{ S_B}{S_A}\)
\(S_A \gg S_B \) donc \(\frac{ S_B}{S_A}\simeq0\) et \( V_A\simeq0\)
D.7 Montrer que la hauteur manométrique totale de la pompe est proche de 8,64 m en appliquant le théorème de Bernoulli entre le puits de stockage (point A) et la station de dépollution (point B). Le point B se situe a l’air libre.
Équation de Bernoulli pour un fluide en écoulement permanent d’un point 1 vers un point 2 :
\(z_1+\frac{p_1}{\rho \times g}+\frac{v_1^2}{2\times g}-J+H_{mt} = z_2+\frac{p_2}{\rho \times g}+\frac{v_2^2}{2\times g} \)
L’écoulement qui nous concerne va du point A au point B :
\(z_A+\frac{p_A}{\rho \times g}+\frac{v_A^2}{2\times g}-J+H_{mt} = z_B+\frac{p_B}{\rho \times g}+\frac{v_B^2}{2\times g} \)
Les données sont :
\( V_A=0\), \(P_A = P_{atmo}\)
\( V_B=3,54\, m \cdot s^{-1}\), \(P_B = P_{atmo}\)
« Les pertes de charge sont équivalentes a une hauteur de 1 m de liquide. » donc J =1m
La valeur charchée est : \(H_{mt}\)
A partir de l’équation de Bernoulli, nous pouvons écrire :
\(H_{mt} = z_B+\frac{p_B}{\rho \times g}+\frac{v_B^2}{2\times g}-(z_A+\frac{p_A}{\rho \times g}+\frac{v_A^2}{2\times g}-J) \)
puis, en regroupant les termes par nature :
\(H_{mt} = (z_B-z_A)+\frac{(p_B-p_A}{\rho \times g}+\frac{v_B^2-v_A^2 }{2\times g}+J \)
Remarquons maintenant que :
\(P_A=P_B=P_{atmo} \) donc : \(P_B-P_A=0\)
\( V_A=0\)
Nous pouvons simplifier l’équation de bernoulli :
\(H_{mt} = (z_B-z_A)+\frac{v_B^2 }{2\times g}+J \)
Application numérique : mais où les valeurs de \(Z_A\) et \( Z_B \) sont elles indiquées ???
« Les eaux usées récupérées dans un puits de stockage doivent être relevées d’une hauteur de 7m » donc \(\ Z_B-Z_A =7\, m \)
\(H_{mt} = 7+\frac{3,54^2 }{2\times g}+1 \)
Par ailleurs :
Masse volumique des eaux usées : \( \rho = 1,02 \times 10^3 \, kg·m^{-3}\)
lntensité de la pesanteur : \(g = 9,81 N·kg^{-1}\)
Donc : \(H_{mt} = 7+\frac{3,54^2 }{2\times 9,81}+1 \)
Soit \(H_{mt} = 8,64 \,m \)
Nous obtenons la valeur indiquée dans la question.
D.8 Calculer la puissance hydraulique que doit fournir la pompe.
« Puissance hydraulique d’une pompe de hauteur manométrique totale Hmt, assurant un debit de fluide \(Q_v\) :
\(P=Q_v \cdot \rho \cdot g \cdot H_{mt}\) »
Par ailleurs : Masse volumique des eaux usées : \( \rho = 1,02 \times 10^3 \, kg·m^{-3}\)
Application numérique :
\(P=0,111 \cdot 1,02 \times 10^3 \cdot 9,81 \cdot 8,64\) »
soit P = 9606 W
La pompe doit fournir une puissance hydraulique égale à 9606 W